13. Building the transformation matrix

2D Catenary & Cable Structures
1

Questions and discussion for this lecture live here. Fire away by hitting Reply below :fire:

2

I just want to summarize what I understand:
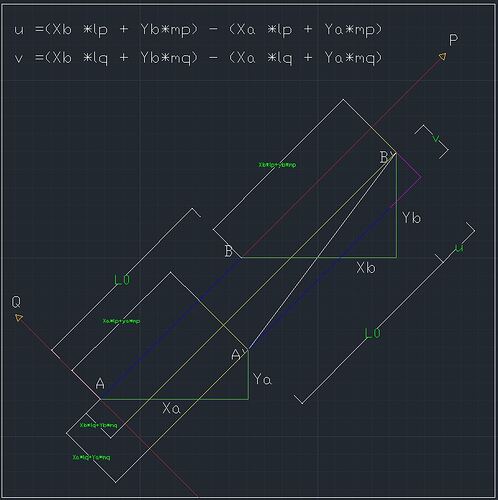
The transformation matrix results in the projection of the deformed configuration onto the undeformed configuration’s local axes (P and Q). The attached image might help illustrate this projection.

projection of the deformed configuration
projection of the deformed configuration908×911 71 KB

3

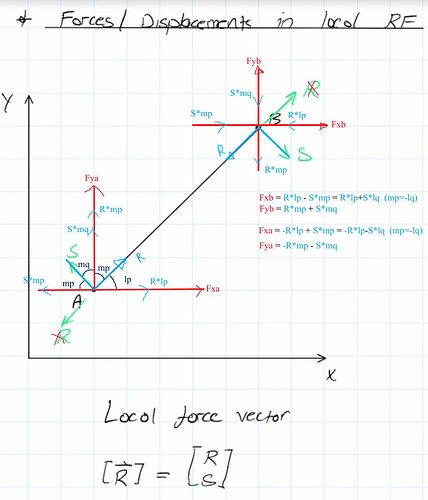
I think the direction of the local force (R) needs to be inverted for the figure to match the equations. Attached are the local forces projected onto the global coordinates.

local forces modified
local forces modified966×1127 78.3 KB

4

Hey @yousif.ali,

I think the confusion may stem from what we define as a positive and negative direction. The local axial force R is shown as a tension force, which is implicitly defined as positive in the local reference frame.

You’ll get to this later in the course…but we can much more clearly see how all of this shakes out with a numerical example.

Consider an element that experiences a 10N axial tension force - R in this case is pointing in the direction shown in the lecture and is a positive quantity (in its reference frame).

If we define the transformation matrix as shown and use it to calculate the corresponding global forces, we see that the global forces are rendered in the correct direction in their global reference frame - i.e. the transformation matrix is performing as expected, mapping quantities from a local to global RF and respecting their respective sign conventions.

I include a minimal code example below for you to inspect.

import numpy as np
import math

def calculateTransMatrix(posI, posJ):
    """
    Take in nodal coords and return the transformation matrix
    """
    ix = posI[0]
    iy = posI[1]
    jx = posJ[0]
    jy = posJ[1]
    
    dx = jx-ix
    dy = jy-iy
    lo = math.sqrt(dx**2 + dy**2)
    lp = dx/lo
    mp = dy/lo
    lq = -mp
    mq = lp
    
    T = np.array([[-lp, -mp, lp, mp],[-lq, -mq, lq, mq]])
    return T  

#Calculate the transformation matrix for the element
TM =  calculateTransMatrix([xa, ya],[xb, yb])

r = 10 #Tension force (+ve) - arrow pointing out of element as shown in lecture
s = 0 

#Local force vector
R = np.array([[r],[s]])
FG = TM.transpose()@R
print("The global force vector:")
print("")
print(FG)

This code block outputs:
The global force vector:

[[ 7.07106781]
[ 7.07106781]
[-7.07106781]
[-7.07106781]]

Note the directions of the force components at each end of the member.

I hope this helps to clear things up for you.
Seán