Hi All,
After a couple of weeks buried deep in code, I thought I should come up for air and give you an update on my progress developing code for the next course - Non-linear analysis of cable and catenary structures.
The first thing I’ve realised is that this topic is huge - so I’m going to split the course into 2 separate courses, one for 2D and for 3D structures. This will mean I can get a course out to you quicker - and it’s actually helpful to break up the challenge for people tackling the topic (and me developing the code ![]()
The 3D course, in particular, has a lot of potential to work in some really interesting Blender content for form-finding and visualisation. If you follow Blender development or are part of that community, you’ll have heard about the recent release of Geometry Nodes - this has massive potential for us using Blender as a structural modelling and data visualisation tool - so much to explore with you here!
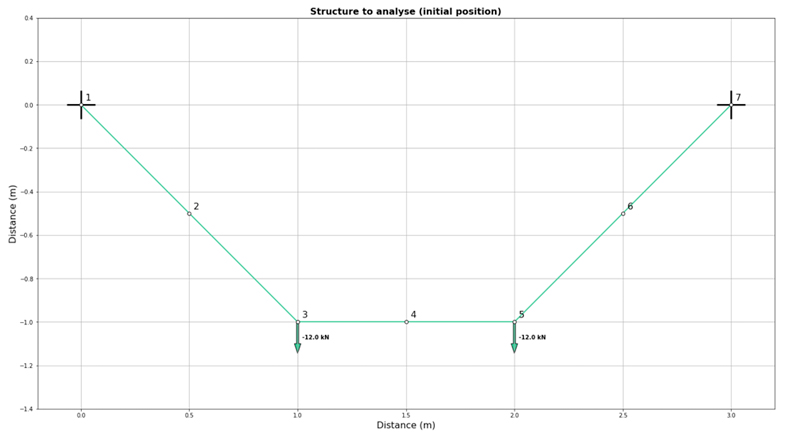
So, as a quick demo of where I’m up to, take this simple 6-element catenary with two 12 kN point loads as shown below. You can think of this as a really low-fidelity approximation of a cable.
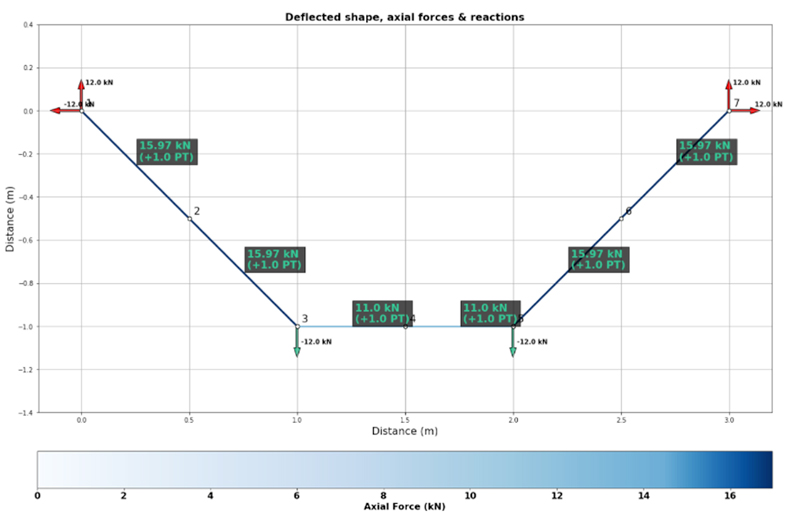
If the axial stiffness of the elements is sufficiently high, then the displacement will be small relative to the scale of the structure (deflections are imperceptible in the image below). In this case, the new non-linear analysis code I’m working on basically performs a linear analysis and we see the result we’d expect…equal magnitude horizontal and vertical reactions because the hangers are orientated at very close to 45 degrees, even when the structure has deflected.
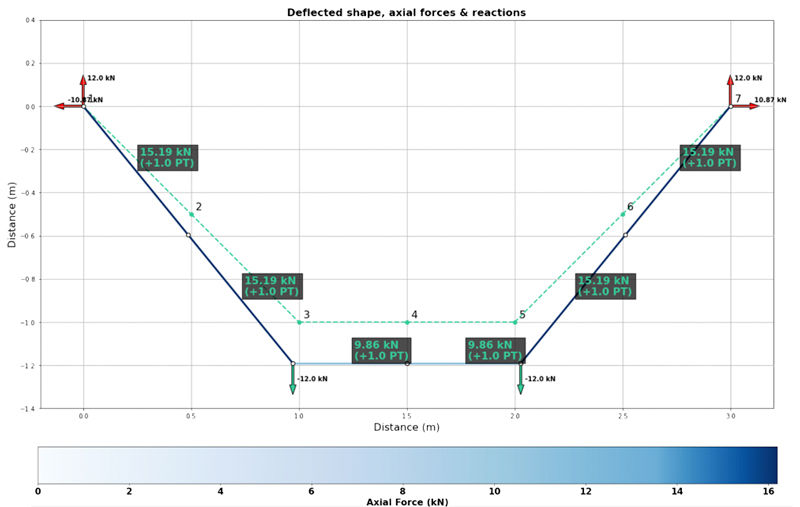
However, if we radically reduce the axial stiffness, the deflection becomes large and the force distribution within the structure is influenced by the deformed shape of the structure - this requires a non-linear analysis and is where things get tricky!
Notice below, how the vertical reactions are larger than the horizontal reactions due to the different angle the hanger makes in the deformed position. The internal force distribution within the structure has also changed as a result of the deflection - this is classic geometric non-linearity.
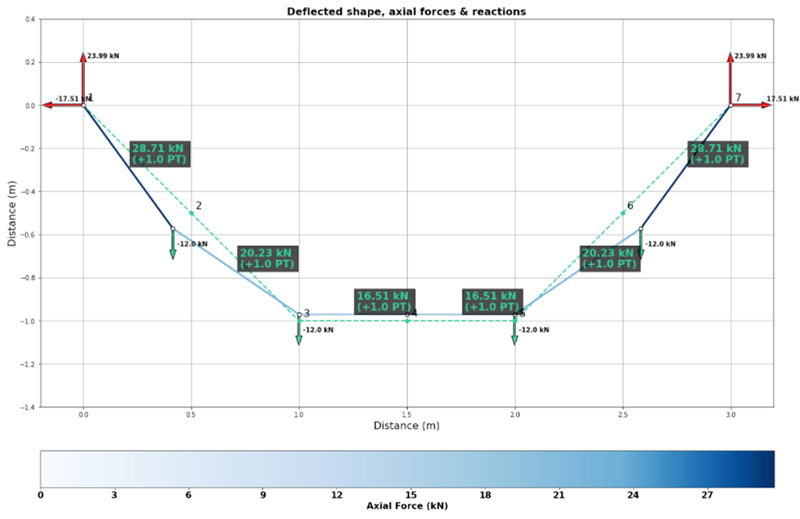
However, if we want to make things really tricky, we can also induce large deflections by adding two more point loads on nodes 2 and 6. So, if we now restore the original axial stiffness but add these loads we obtain the following result:
The nice thing about the code that I’ve developed so far is that it’s a single solution algorithm that will accommodate linear and non-linear structural behaviour. There is still plenty to do and a lot of technical challenges to overcome so I’m still very much in development mode - I’ll keep you updated on progress though.
If you’re keen to take this course when it’s released and want to make sure you’ve covered the prerequisite material, make sure to complete the 2D (linear) truss analysis course. That will leave you well placed to get started on the 2D non-linear course when I release it.
That’s all for this update - it’s back to the debugging for me!
Speak soon,
Seán