Questions and discussion for this lecture live here. Fire away by hitting Reply below ![]()
Dr Sean,
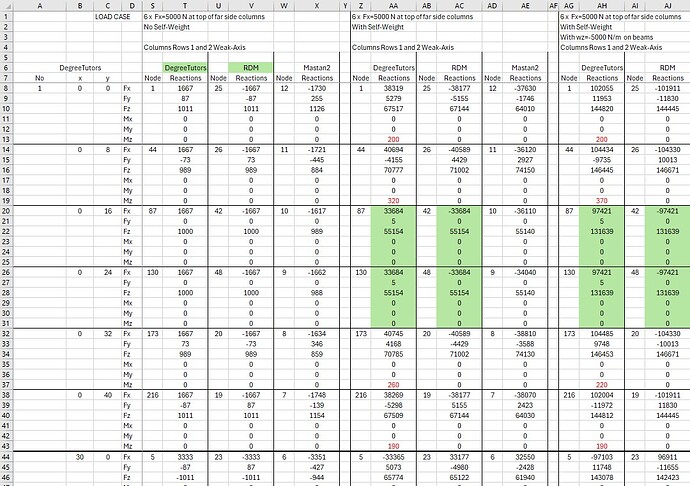
At 10:31 when we see reactions on the Axial Forces Diagram, I remarked that there is a small moment about z-axis at nodes 44, 48, 173 and 177. As there is no rotational restraint at these nodes, there shouldn’t be any moment there. I compared the Notebook’s results with the results of RDM [https://iut.univ-lemans.fr/ydlogi/rdm_version_7.htm]. For different combination of load cases (lateral force, UDL, self-weight, columns strong and weak-axis), I found the results very similar except when self-weight is applied in braced bay. The reactions at frames between braced bays are identical with or without self-weight.
Do you have idea where these small moments come from?
Hi @Tom1961,
Yes, there should be zero moment reactions about all axes, as you say. At first glance I’m not sure why there is a small non-zero Mz value for some of the pinned supports.
I’ve being digging into the code a little and it seems the appearance of the Mz moment is related to the bracing members being axial-only members as the moments are eliminated if we do not designate these as axial only and instead leave them as beam elements.
I haven’t had time to get to the bottom of this and I’ll be travelling all next week but I fully intend to return to this when I get back and update this thread. In the meantime, if you manage to trace the issue - do please update the thread.
Also, I wasn’t sure what you meant when you said…
The reactions at frames between braced bays are identical with or without self-weight.
I didn’t observe this and may have misinterpreted you - could you elaborate?
Thanks,
Seán
Hello Sean, for the interior bays, when I said the reactions were identical with and without self-weight, I wanted to say the reactions are identical to the ones calculated by RDM, which was my reference.
According to your answer, I will investigate the axial only braces on my side.
Thanks for your commitment in providing answers
Hello Sean, I think that I have found the problem and the solution. In section 21.0, there is a check to make sure the sum at the row of each pinned DoF is zero before including this DoF in pinDoF_empty. I have found that some DoF (e.g. the ones at supports) have a sum less than close to zero.
I tried to change the check for the absolute number of the sum in case the sum was negative and then < 0.00001. This was not the case. The DoF in pinDoF_empty remained unchanged with the new code line.
I tried then to make the sum of absolute number of each element in the row , in case there were two values equal but with opposite sign. The unwanted DoF in pinDoF_empty disappeared. I compare the new results with RDM, as I did before, and get exactly the same results with no more moments where it souldn’t be.
To check the results, I worked with a simplified model with only 3 bays and very few members. I can provide the csv files if desired as well as the Excel file for the comparaison with RDM.
Here is the change I did in the code of section 21.0:
sumCheck = np.sum(abs(Kp[p,:]))
Please confirm this solution is correct and resolves the problem encountered.
Hey @Tom1961,
Thanks for your patience while I was away last week! TBH, I’m glad you had the time to work on this because you’ve identified and fixed the bug! ![]()
![]()
![]()
My original check in code block 21 (line 7)…
sumCheck = np.sum(Kp[p,:])
…did not capture the case where (as you point out) opposite sign contributions effectively cancel each other out and are missed by the check, leading to the unintended removal of additional rows and columns from the stiffness matrix!
Thanks for proposing the following fix, that I fully endorse…
sumCheck = np.sum(abs(Kp[p,:]))
This results in a check that is actually in line with what I intended ![]()
Thanks again - I very much appreciate your contribution on this.
Seán