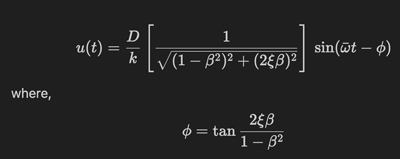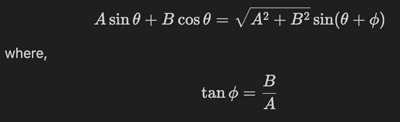Questions and discussion for this lecture live here. Fire away by hitting Reply below ![]()
Hello Sean,
Could you help clarify what’s happening at the boundary where beta = sqrt(2)?
Also, why doesn’t this phenomenon occur for the Dynamic Magnification Factor with respect to the static response?
Thanks
Hi,
I’m afraid I don’t have a more intuitive explanation for what’s happening at the boundary beta=sqrt(2), beyond simply that it is an emergent behaviour of the system, i.e. it’s one of those things predicted by the mathematics that we otherwise would be unlikely to intuit (not particularly satisfying, I know). I’ve reviewed several texts on the topic and there is little further explanation beyond this.
In terms of the DMF, while there is some obvious similarities between it and transmissibility it’s still important to remember that one (DMF) is a ratio of a steady-state oscillation amplitude to a static deflection and the other is a ratio of steady state amplitudes of two separate but linked SDoF systems. So, in that regard it is not all that surprising that we don’t observe this same ‘cross-over’ point of beta=sqrt(2) that all curves pass through.
However, we do observe that for certain frequency ratios, we can obtain DMF values less than 1, i.e. we would observe a steady state response less than the equivalent static response. So, a harmonic force can have both a positive and negative magnifying effect - which is not dissimilar to what happens on either side of the transmisibility boundary.
Not a complete answer but hopefully somewhat helpful.
S
Hi Sean,
I have a simple question :
How did we come up with a squareroot here ? I mean our steady state response amplitude which we denoted as U does not have a squareroot in the denominator. Therefore, i was expecting the transmissibilty formula as below :
$$T = \frac{\sqrt{1+(2\xi\beta)^2}}{(1-\beta^2)^2 + (2\xi\beta)^2}$$
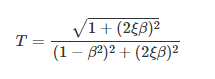
i am little confused about that. I guess this is happening because you are taking out 1-\beta^2 and -2*\xi\beta from sin and cosine terms as a amplitude from u(t) in other words you are defining U(t) as = $$ U(t) = U [\sin(\bar\omega +\gamma) + \cos(\bar\omega+\gamma)] $$
![]()
Could you please have a look once you have a chance ?
Cheers,
Thanks a lot ,
Burak