Questions and discussion for this lecture live here. Fire away by hitting Reply below ![]()
Hello Sean,
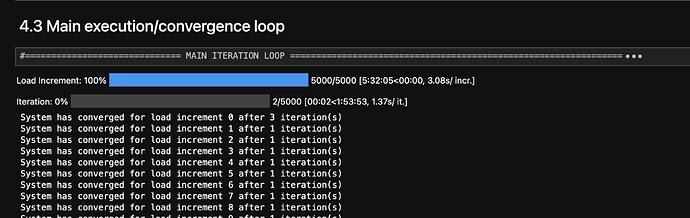
I want to share a small tool that I implemented in my solver to provide a progress bar while the solver is calculating. The implementation is very simple and for long calculations, it provides a quick view of the progress and the required information to estimate the duration of the calculation.
For this lesson, my computer worked hard for 5.5 hours to run the 5000 load increments.
There are 2 progress bars. One for the iteration count and one for the increment count. Look for ‘pbar_i’ and 'pbar_inc 'in the code. Also in Dependencies, need to import
from tqdm.notebook import tqdm, trange #Allow for adding progress bar in convergence loop
#============================== MAIN ITERATION LOOP ================================================================
i = 0 #Initialise an iteration counter (zeros out for each load increment)
inc = 0 #Initialise load increment counter
notConverged = True #Initialise convergence flag
#Progress bar (requires tqdm import: see Dependencies)
pbar_inc = trange((nForceIncrements_sw + nForceIncrements_ext), desc=' Load Increment', unit=' incr.')
pbar_i = trange(itLimit, desc=' Iteration', unit=' it.')
while notConverged and i<itLimit:
#Calculate the cumulative internal forces Fi_total = Fa + Fb + Fc + ...
Fi_total = np.matrix(np.sum(F_inc, axis=1)).T #Sum across columns of F_inc
#Calculate the cumulative incremental displacements UG_total = Xa + Xb + Xc + ...
UG_total = np.matrix(np.sum(UG_inc, axis=1)).T #Sum across columns of UG_inc
#Inequilibrium force vector used in this iteration F_EXT - Fi_total or externalForces - (cumulative) internalForces
F_inequilibrium = forceVector - Fi_total
#Build the structure stiffness matrix based on current position (using cumulative displacements)
Ks = buildStructureStiffnessMatrix(UG_total)
#Solve for global (incremental) displacement vector [Xn] for this iteration
UG = solveDisplacements(Ks, F_inequilibrium)
#Calculate a new transformation matrix for each member based on cumulative displacement up to previous iteration
TMs = calculateTransMatrices(UG_total)
#Calculate the internal force system based on new incremental displacements. [Fn]
F_int = updateInternalForceSystem(UG)
#Save incremental displacements and associated internal forces for this iteration
UG_inc = np.append(UG_inc, UG, axis=1)
F_inc = np.append(F_inc, F_int, axis=1)
#Test for convergence
notConverged, maxIneq = testForConvergence(i, convThreshold, F_inequilibrium)
i += 1
pbar_i.update(1) #Update iteration progress bar by one iteration
if i == itLimit:
print(f'🛑 ATTENTION: No convergence after {itLimit} iterations')
#If system has converged, test for slack elements, save converged displacement, forces and increment external loading
if not notConverged:
hasSlackElements = False #Initialise a flag to indicate presence of new slack elements
mbrForces = calculateMbrForces(UG_total) #Calculate member forces based on current set of displacements
if inc > checkSlackAfter:
for m, mbr in enumerate(members):
if (memberType[m] == 'c' and mbrForces[m] < 0):
print('--------------------------------------------------------------------------------------------------------------\n',
f'Compression in cable element from nodes {mbr[0]} to {mbr[1]}\n',
'---------------------------------------------------------------------------------------------------------------',)
hasSlackElements = True #Switch slack element flag
Areas[m] = 0 #Eliminate member stiffness by setting its section area to zero
P0[m] = 0 #Eliminate pre-tension
if not hasSlackElements:
print(f'System has converged for load increment {inc} after {i-1} iteration(s)')
#Save a 'Snapshot' of the system at this converged load increment
UG_FINAL = np.append(UG_FINAL, UG_total, axis=1) #Add the converged displacement record
UG_inc = np.empty([nDoF,0]) #Zero out the record of the incremental displacements for the next load increment
UG_inc = np.array(np.append(UG_inc, UG_total, axis=1)) #Add the initial displacement record for the next load increment (manually cast as ndarray instead of matrix)
FI_FINAL = np.append(FI_FINAL, Fi_total, axis=1)#Add the converged force record
F_inc = np.empty([nDoF,0]) #Zeroout the record of incremental forces for the next load increment
F_inc = np.array(np.append(F_inc, Fi_total, axis=1)) #Add the initial force record for the next load increment (manually cast as ndarray instead of matrix)
mbrForces = calculateMbrForces(UG_FINAL[:,-1])
MBRFORCES = np.append(MBRFORCES, np.matrix(mbrForces).T, axis=1) #Add the converge axial force record
EXTFORCES = np.append(EXTFORCES, forceVector, axis=1) #Add the external force vector for this load increment
#Add another external force increment
if abs(sum(forceVector).item()) < abs(sum(maxForce).item()):
i=0 #Reset counter for the next load increment
pbar_i.reset() #Reset progress bar counter to 0
inc += 1 #Increase load increment counter by 1
pbar_inc.update(1) #Update progress bar by 1 increment
#Apply the self-weigth increments first then the external loads
if inc < nForceIncrements_sw:
forceVector = forceVector + forceIncrement_sw #In=crement the self-weight
else:
forceVector = forceVector + forceIncrement_ext #Increment the applied forces
notConverged = True #Reset the notConverged flag for the next load increment
else:
print('----------------------------------------------------------------------------------------------------------------------\n',
'Re-run the load increment with slack element (cable) stiffness set to zero\n',
'------------------------------------------------------------------------------------------------------------------------')
F_inc = np.empty([nDoF,0]) #Zeroout the record of incremental forces for the next load increment
F_inc = np.array(np.append(F_inc, FI_FINAL[:,-1], axis=1)) #Reset F_inc to values from previous converged load increment
UG_inc = np.empty([nDoF,0]) #Zero out the record of the incremental displacements for the next load increment
UG_inc = np.array(np.append(UG_inc, UG_FINAL[:,-1], axis=1)) #Reset UG_inc to values from previous converged load increment
#EXTFORCES contains P0, that is indirectly eliminated when setting area of member to zero.
forceVector = np.array([EXTFORCES[:,-1]]).T #Reset the external force vector to last converged value
i=0 #Reset counter for the next load increment
pbar_i.reset() #Reset progress bar counter to 0
notConverged = True #Reset notConverged flag for the next load increment