Questions and discussion for this lecture live here. Fire away by hitting Reply below ![]()
Hi @Sean,
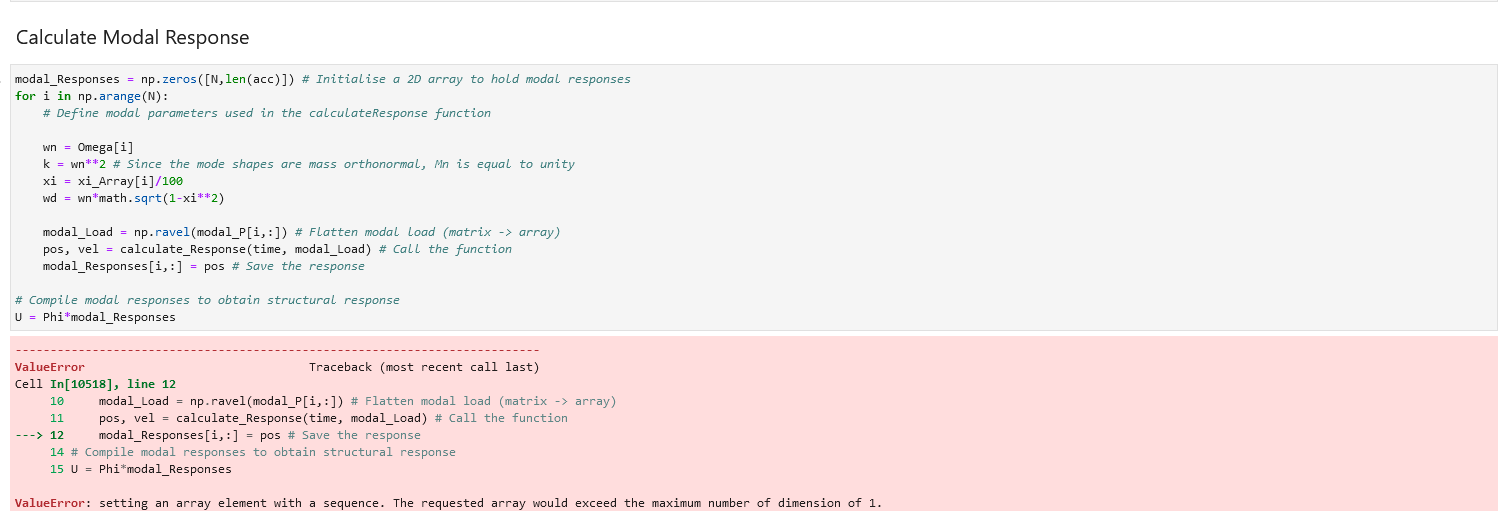
I am running Lecture 37 script with a 15 story building as well as importing random ground motions.
I have been unsuccessful fixing the 1D error below:
Hi @asiric80, have you been able to run the code that comes with the course? It’s attached to lecture 35.
S
Hi Sean,
I resolved the error - it had to do with my array matrix dimensions.
Additionally, my animation is working perfectly! I think these links might be of interest to students having the same animation errors I encountered:
https://jckantor.github.io/CBE30338/A.03-Animation-in-Jupyter-Notebooks.html
On another note, i have successfully simulated a 15 story building dynamic response using random ground motions via a LHS MC simulation import - fun work!
Fantastic! And thanks for posting those links!
S
Hi!
I am having the same dimensional error you encountered, can you explain what you did to solve it?
Thanks!
Hello Sean,
In the calculation of the effective inertia forces, the ground acceleration is simply multiplied by the mass of each floor:
Peff = np.zeros([N, len(acc)])
for i in np.arange(N):
Peff[i, :] = -acc * mArray[i]
My question is: Does this approach realistically distribute the earthquake forces to each floor? Would it be more appropriate to distribute the forces according to the first mode shape or another loading pattern? How could an alternative loading approach be implemented?
Hi @mrgurer
Any inaccuracy in this approach stems from the inaccuracy in the mass distribution - i.e. the fact that lumping all mass at floor levels is itself a simplification. It’s left to the judgement of the engineer to determine just how important this simplification is, given the particulars of a given project - but it’s not a bad starting point.
Determining an inertia force by multiplying mass by acceleration is perfectly valid.
In terms of identifying an alternative approach - I’m not sure what you mean…there is always more refined finite element modelling - but the fundamental dynamics won’t change.
Hope that helps.
Seán