Questions and discussion for this lecture live here. Fire away by hitting Reply below ![]()
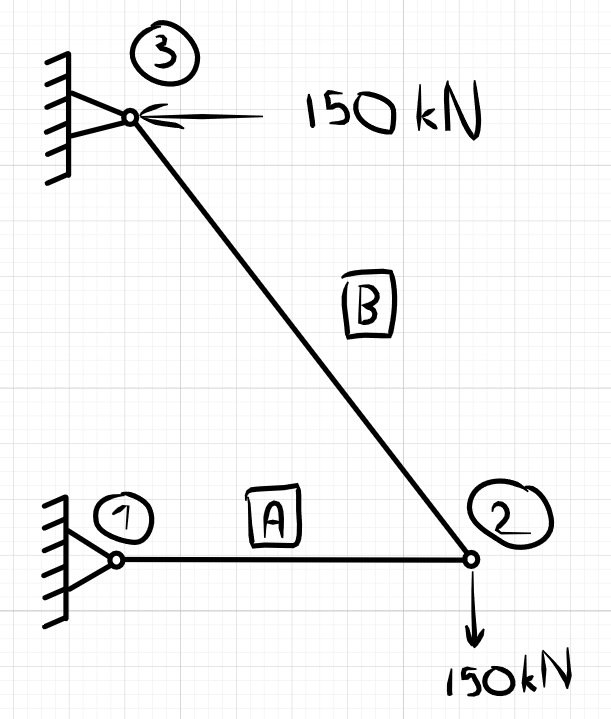
Hi! The question isn’t exactly on the topic of this video, but if I try to apply horizontal force to the node 3 with pinned support from your example, I’ll get reaction forces of node 3 without impact of new applied force. Do we need additional equations to take into account external forces applied to any support?
Hi, you’re right that the horizontal force at node 3 is directed straight into the support and this will be reflected in the reaction at node 3. However, the vertical force at node 2 will also have an influence on the reaction at node 3.
For example, taking the sum of the moments about node 1, will yield the reaction at node 3 that captures the influence of both externally applied forces.
S
Thanks for your reply! I guess my question wasn’t very clear. What I meant was, if I follow the algorithm from the video, then at the stage of applying boundary conditions, I place a 1 in the stiffness matrix diagonal corresponding to the known zero displacement, and 0 in all other elements of the corresponding rows and columns. I also place a 0 in the corresponding elements of the force vector. However, by doing this, I end up with an incorrect reaction force vector when solving the equation for unknown reactions with the primary stiffness matrix. The equation turns out to be exactly the same as in the video, leading to the same reaction forces.
Am I missing something or misunderstanding?
Ah I understand what you’re asking now. The stiffness method procedure we implemented assumes that all forces are applied on nodes of the structure and NOT onto supports. Therefore, if you want to capture the influence of the horizontal force on the reaction at node 3, you must add it manually.
Applying a force directly to a restrained node is the same as applying that force to the ground adjacent to the structure…it has no influence on the structure itself…i.e. it induces no stresses within the structure.