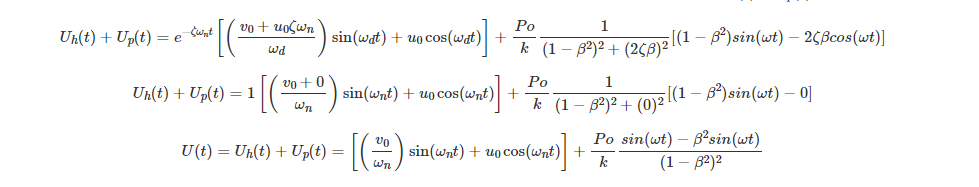Questions and discussion for this lecture live here. Fire away by hitting Reply below ![]()
Hello Sean,
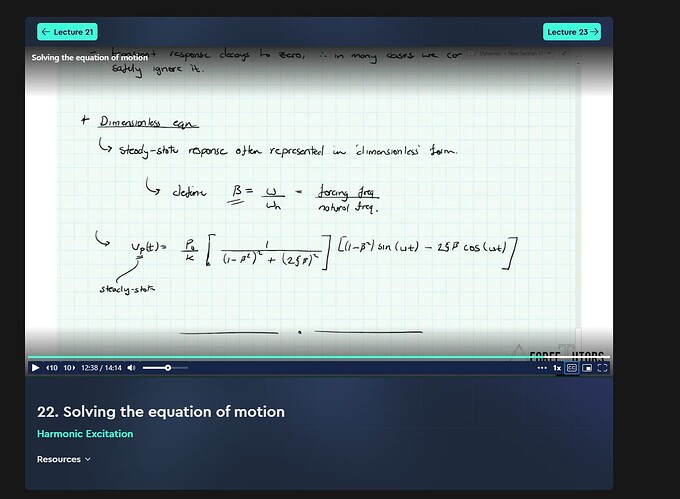
First of all, I may be wrong with my observation. However, something did not settle in my mind properly. At 8:32/9:30 range in the video, we are saying that transient response never dies away. However, as far as I understood in fundamentals of dynamics class, the full solution shall be Transient + Steady State Solution. (Fundamentals of Engineering Structural Dynamics with Python, Section 3, Video 22, Solving the Equation of Motion, 12:38)
Considering there is no damping in our case for this video, both shall appear. However, I see only steady state response without damping in this case. Am I missing something here ?
Thanks a lot in advance,
Sincerely,
Burak
Hey Burak,
Indeed, both the steady state and ‘transient’ response do appear - equation 6 in the text accompanying lecture 24 actually represents both parts of the response. Note that we have both frequency terms in there, omega - representing the forcing frequency and therefore the forced response, and omega_n, representing the free vibration response.
Of course, when we say ‘transient’, in this case this part of the response is not transient since the damping is zero and therefore this component of the response never dies away. This is a fictional case, since there will always be some degree of damping in reality.
One final note - you should try to derive equation 6. If you do so, it will be helpful to know that equation 6 is for the case when the initial position and velocity is zero.
I hope that helps!
Seán
Cheers a lot Sean, as you said i inserted initial position and velocity as 0, and damping ratio as 0, and the equation 6 totally derived. Now it is crystal clear for me.
Without deriving the equation at first glance, it felt like that we skipped the transient response experession, but not all actually.
Thanks a lot,
Burak
Hi Sean @Sean , for the derivation of the response i am kinda confused. I know this is actually very hypotetical case with zero damping, but maybe i am missing something crucical. Could you please have a look to below screenshot where i derive the reaction of our system with zero damping to harmonic force as we say, U(t)? Time in video : 8:25
And actually, if that would be the case we would need the initial conditions to have the response of our system as per my derivation lets say. Confused kinda little bit.
I realized i asked a very similar question before, so the answer for this derivation that when initial conditions are 0, we get the version which you have written then ? @Sean
Thanks a lot,
Burak
Hey @m.burakcakir33 - just to clarify…are you asking what would equation 6 look like if we did not assume zero initial velocity and displacement?
In other words, what would the equation look like if the initial position and velocity we retained as variables in the equation?
To get this equation, we just solve the equation of motion (as we did here), but with the damping term set to zero. When you do this, and also set the initial conditions to zero, you get equation 6 in the lecture notes. But you can just as easily retain u_0 and v_0 as variables.
S