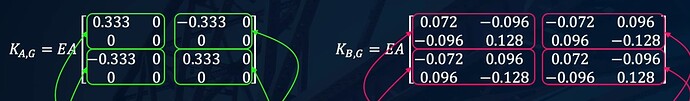21. Building the primary stiffness matrix

[Sean]

Questions and discussion for this lecture live here. Fire away by hitting Reply below

[Biagio74]

When you filled in the stiffness matrix template with the element’s stiffness matrices quadrants, and get the overlap between the green and pink area; why the pink is dominating? With other words, why the member B values have been populated to the template and not the member A values?

[Sean]

Hey,
I’m not sure I follow completely…

No single element dominates when filling in the primary stiffness matrix (PSM). The contribution from all elements are simply added to their respective locations in the PSM.

If this hasn’t helped clear things up, perhaps leave a timestamp to the time in the video that your question relates to…this will help me give a better answer.

Cheers,
Seán

[Biagio74]

@Sean

this lecture

thanks for the explanation, however it is still not clear for me. So, if I take both K_A,G and K_B,G from time 1:32 in the lecture, as below:

…then I would expect to fill in the template with these ones at around 5:20 in the lecture. But in the quadrant K_A22 I see different values respect to the ones in the previous slides.

With other words, why the the quadrant K_A22 values become [0.405, -0.096; -0.096, 0.128] from [0.333,0; 0,0]
So I still see K_A22 competing with K_B11 for the same place in the overlapping area in the stiffness matrix.

[Sean]

Hey,
This is because when we generate the primary stiffness matrix, some of the values will actually be the superposition of individual values from the element stiffness matrices. This is the beauty of the method…we can build up the overall primary stiffness matrix by simply ‘overlaying’ the contribution from individual members within the structure.

So to obtain the values in the overlapping area of the primary stiffness matrix we add K_A,22 and K_B,11. This makes sense as these degrees of freedom are common to both elements…since they are connected together at node 2.

Let me know if you still find this confusing.

Seán

[Biagio74]

ok, got it now, overlaying means basically just an addition of the two in the overlapping area …I was completely off, just looking at the -0.096 and never realised that K_A22 has zero values in the same place, so producing the same value.

[Sean]

Now you have it - once you’ve understood this concept of ‘building up’ the stiffness matrix, it generalises to many many more analyses.
Seán

[Biagio74]

Yess, very much make sense. …above all, by now, after the Truss 2 Question exercise gave a lot of understanding working alone on the problem. Due to the larger structure (6 nodes, 8 members) it gave the concept how to fill in the template stiffness matrix. And also, how to work at “scale” with the matrices and vectors.

And the result is so satisfying

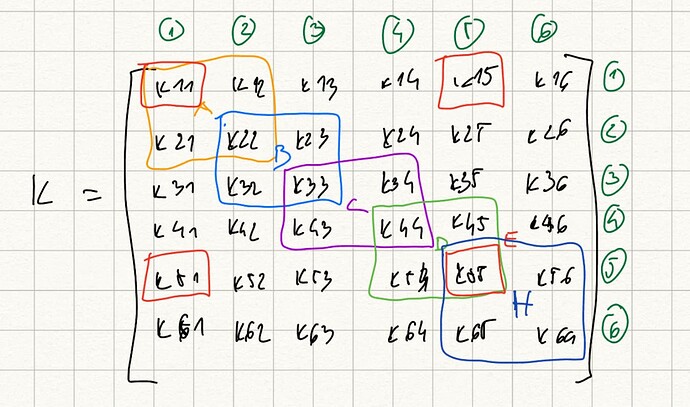
PS.: And at some point (when solving for displacement) I got an error, the famous error which we used to get in FEA solvers a Singular matrix …I couldn’t invert matrix Ks because I forgot to include member F and G in my primary stiffness matrix. So Ks.I couldn’t run. So my structure didn’t make sense with only bar members.
I used the below draft for myself, but you may see that those two membrs are missing. …such a nice experience

[Sean]

Great to hear you’re enjoying the course! Yes…something very satisfying about coding up a solution to a structure that would be unfeasible to solve by hand.

Ah yes, the good old singular matrix…won’t be the last time you hit that !

Keep it up!
Seán