Questions and discussion for this lecture live here. Fire away by hitting Reply below ![]()
I was having trouble with the animation (in this lecture and all following lectures which included animation) and getting an error: “Javascript Error: IPython Is Not Defined”. I made the following change and it started working (but I will say I’m new to Python so I’m not sure if this is a good fix).
%matplotlib notebook
Changed to:
%matplotlib widget
Also, I often had to restart the entire kernal if making any changes to any plot, otherwise the same error would occur when using matplotlib.
Thanks for posting this update Dan, much appreciated.
S
Hello Sean,
I’m curious about why we don’t include phase angle terms in the response of masses. By not having separate phase angle variables for each mass, it seems we are limited to only 0 or 180 degrees of phase shift between the responses. Does this assumption always hold true?
I’d appreciate any insights you can provide.
Thanks!
Hey @Shakib.Ayoubzadeh - remember that the modal responses are at different frequencies - as such, phase angle is not a meaningful parameter in this context as phase is only something we measure between oscillations of the same frequency.
S
Hi Sean @Sean,
As usual, thanks a lot for incredibly useful and insightful content.
I did not understand one crucial part i believe which is the following :
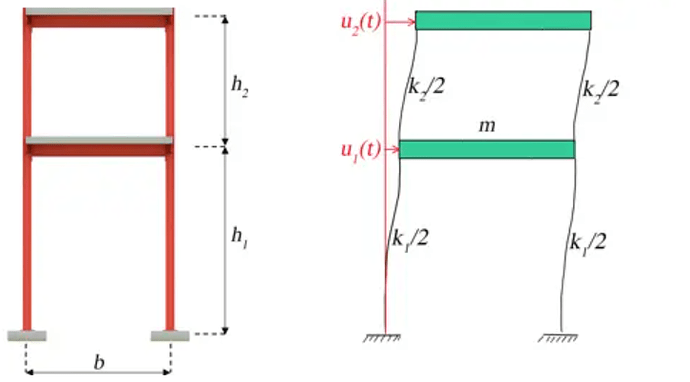
1- While we are making lumped masses for each DOF in our code we are using the top half of the first floor columns and bottom half of the second floor columns which totally makes sense. However, for the stiffness i am kinda confused, i was expecting the same mentality, but it is not the case. To be clear let me note it down the codes for the mass and stiffness :
Stiffness :
k1=2(12EIx_254/h13)*
k2=2(12EIx_203/h23)*
**m1_cols= (h1/2)2gamma_UC254 + (h2/2)2gamma_UC203 **
#### MASS OF HALF OF COLUMNS BELOW AND ABOVE OF LEVEL 1
m2_cols= (h2/2)2gamma_UC203
#### MASS OF HALF OF COLUMNS BELOW LEVEL 2, 1/2 * 2 h2gamma_UC203
I understand that stiffness is proportinal to L^1/3 so numerically we cannot do the same like mass, but with playing with ratios, i was expecting the same behaviour. What is the main reason we consider this difference for the lumped mass and stiffness case ?
I am sorry that i ask so many questions, i am just trying my best to digest all information i get from your lectures. Thanks a lot for your efforts and time to explain it as always.
Cheers,
Burak
Hey Burak - questions are no problem - they help everyone!
So, to your question; I sort of see your point but on the other hand since we’re modelling two fundamentally different quantities, there is no reason that we should necessarily treat them the same in terms of discretisation.
In the case of stiffness, what controls the motion of m1 relative to the ground is k1 (k2 has no influence here). Similarly, k1 has no influence on the relationship between mass m2 and m1 - so, on this basis, it’s logical to discretise the stiffness of the system as we have.
In terms of mass, we want to lump all mass based on proximity (vertical distance) to our selected lumped mass locations (floor locations). So, again, it’s logical to lump half the column mass above and below a floor.
Hope that helps.
Seán