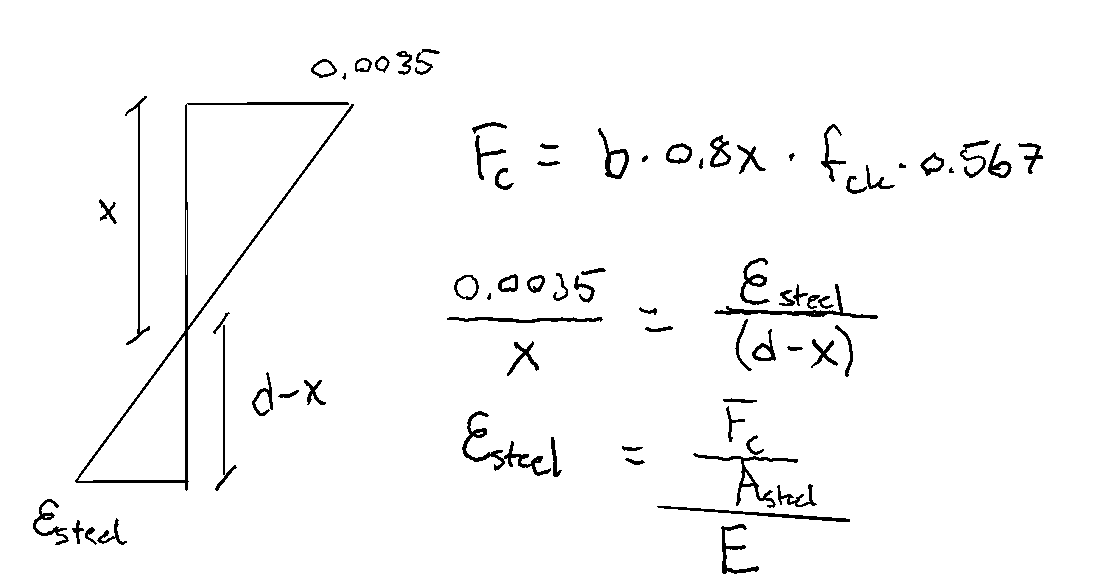Questions and discussion for this lecture live here. Fire away by hitting Reply below 
Hi
First one small detail:
When I try to download the code example, i get an error saying “404, file not available on site”. Is there another way to access the code in a copy-pasteable format, or can the link be fixed?
Also:
When trying to work out the solution by myself, I came up with a solution that is wrong, but not very wrong, and I don’t understand why. Maybe someone could help point out which wrong assumption I’m making, and why exactly it is necessary to take an iterative approach to finding the neutral axis depth. I see that it is very clearly the easiest way, but I’d still like to understand why the other solution isn’t correct.
My thinking was based on the strain curve shown below
I thought that the Force in the concrete was given as a function of x, and that the strain in the steel could be expressed as (Fc/As)/Es. -Stress divided by the elastic modulus for steel.
I also thought that the slope of the line would be the same on each side of the neutral axis. so I expected the respective strains over the distances x and (d-x), (rise over run) to be equal. Solving for that, I get the results below:
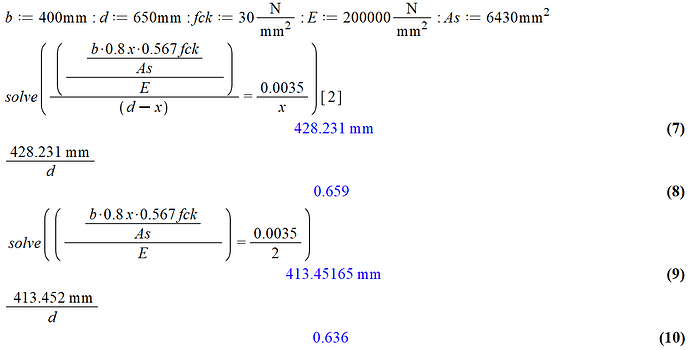
As you can see, that gives me a value of 428 mm, which is not very far off, but definitely not correct.
Where things become even stranger for me is in the expression below, which I stumbled across by mistake, solving for the steel strain being equal to half the concrete strain. Solving this, I do get the correct, or very nearly correct value. Can anyone explain why this is the case, and whether it’s widely applicable in theory?
Best,
Hektor
Hey @hektorsabroe,
First off - thanks for alerting me to the issue re. file downloads - this is fixed now (yesterday in fact). You shouldn’t have any trouble downloading files now.
Now, re. your second question…you are correct! You don’t need to solve this problem using iteration - this is just how I have always done it, but there is nothing wrong with solving for x algebraically as you have correctly done. I need to make this clear in the lecture and will be updating the lecture shortly to reflect this.
After being taught this many moons ago - I never thought about it from your angle and always went straight for the iterative method. Nice work pointing out the alternative approach.
The reason your answer for x doesn’t tally with the lecture is that I made an error. When calculating the force in the steel, after we’ve solved for x, the factor 0.87 should be omitted since we are dealing with the working level of stress in the steel at the point of concrete failure (rather than the characteristic yield stress). When this factor is omitted, both the iterative and algebraic solution are in agreement.
Thanks again for raising this - questions like this really help clear things up for everyone else taking the course (and me!).
Seán
To anyone else - if you’re reading this, it means I haven’t yet updated the lecture as per my comment above.
Cool! Thanks a lot for the quick reply Sean! That helps a lot.
Only glad that I can catch a few of the starting bugs with the new website. Love the new look and feel.
Hektor
1 Like
Hi Sean,
Finding the content very helpful! I was just wondering could you explain why we are removing the 0.87 factor from the steel equation but still using the 0.567 factor for the concrete force rather than a factor of 0.85 (excluding 1.5 factor) if it we are using working level stress. Its just confusing me when looking at the algebraic solution with similar triangles in the comments when one is using the material factor and the other isn’t?
Thanks
Matthew
Can you help me out by pointing to the timestamp in the video that was confusing you - I couldn’t find where we dropped the 0.87 factor. I may be misinterpreting your question, happy to look again though if you want to follow up.
Seán
Hi Seán, apologies, I didn’t make it very clear what I was referring to. In hektorsabroes previous comment and in your reply you discussed omitting the 0.87 factor so was just wondering if we are removing that meaning we are dealing with working stress why is 0.67 (1/1.5) factor for concrete not omitted making it ((b0.8x0.85*fck)/As)/E in the same equation. Maybe I have misunderstood something?